Data Structure & Algorithm Solved Paper-2023|Solved Paper-Data Structure & Algorithm-BCA

1. Choose the correct option : (10×1=10)

(i) If an array is declared as int a[5][6], how many elements can be stored in it

(a) 10

(b) 20

(c) 30

(d) None of the above

(ii) While inserting the elements 71,65,84, 69,67,83 in an empty binary search tree (BST) in the sequence shown, the element in the lowest level is

(a) 67

(b) 83

(d) None of the above

(iii) Which of the following is an application of stack

(a) Recursion

(b) Evaluation of postfix expression

(d) All of the above

(iv) Which of the following data structure allows insertion and deletion at two different end?

(a) Queue

(b) Linked list

(d) None of the above

(v) Pop operation in a stack is performed

(a) At the middle of the stack

(b) At the bottom of the stack

(d) None of the above

(vi) Which of the following is the prefix form of A+B*C?

(a) A+(BC*)

(b) +AB*C

(d) +A*BC

(vii) A polynomial equation can be represented using

(a) stack

(b) array

(d) queue

(viii) In Depth First Search, how many times a node is visited?

(a) Once

(b) Twice

(d) Thrice

(ix) The following numbers are inserted into an empty binary search tree in the given order: 10,1,3,5,15,12,16. What is the height of the binary search tree?

(a) 2

(b) 3

(d) 6

(x) Which of the following data structure allows you to insert the elements from both the ends while deletions from only one end?

(a) Output-restricted queue

(b) Priority queue

(d) None of the above

2. (a) Define Data Structure. Differentiate between linear and non linear data structure. (1+2=3)

Ans: A data structure is a fundamental concept in computer science and refers to a way of organizing data in a computer so that it can be accessed and updated efficiently. Data structure is the mechanism of organizing and storing the data properly and establishing the relationship between data stored.

A data structure can be represented as follows:

Data Structure= organized data + allowed operation

Difference between linear and non linear data structure: Linear and nonlinear data structures are two fundamental categories of data structures used in computer science and programming. They differ in how they organize and represent data elements and how data can be accessed within them.

The primary distinction between linear and nonlinear data structures lies in the arrangement of elements and how elements are accessed. Linear data structures have a sequential arrangement with straightforward access patterns, while nonlinear data structures have more complex arrangements with varying access patterns based on relationships between elements.

Differentiation between linear and nonlinear data structures:

Linear Data Structure	Non-Linear Data Structure
In linear data structure, the elements are organized in a linear or sequential manner, meaning they are placed one after the other in a straight line.	In nonlinear data structures, data elements are organized in a way that doesn’t follow a strict linear or sequential arrangement. Elements are interconnected in various ways.
It is single level data structure. All data components are present at a single level.	It is multi-level data structure. Data elements are present at multiple level
Linear data structures are easy to implement.	Non-linear data structures are difficult to implement as compared to the linear data structures.
In linear data structure, data elements can be traversed in a single run only.	In non-linear data structure, data elements can’t be traversed in a single run. It requires multiple runs.
Elements in linear data structures can be accessed in a sequential order, usually from one end to the other. Access is typically straightforward and follows a fixed order.	Accessing elements in nonlinear data structures can be more complex because there isn’t a fixed order.
In a linear data structure, memory is not utilized in an efficient way.	In a non-linear data structure, memory is utilized in an efficient way.
Linear data structures work well mainly in the development of application software.	Non-linear data structures work mainly well in image processing and Artificial Intelligence.
Linear data structures are useful for simple data storage and manipulation.	Non-linear data structures are useful for representing complex relationships and data hierarchies, such as in social networks, file systems, or computer networks.
Common examples of linear data structures include arrays, stacks, queues and linked lists.	Common examples of nonlinear data structures include trees, graphs, and heaps.

(b) What are the disadvantages of array? Explain how linked list overcome these disadvantages? (2+3=5)

Ans: Arrays and linked lists are both data structures used for storing and organizing collections of elements, but they have distinct advantages and disadvantages.

Disadvantages of Arrays:

Fixed Size: Arrays have a fixed size, meaning we need to specify the number of elements they can hold when we create them. This can be limiting if we don’t know in advance how many elements we’ll need.

Contiguous Memory Allocation: In most programming languages, arrays require contiguous memory allocation. This means that all elements in the array must be stored in adjacent memory locations. This can lead to memory fragmentation and limit the availability of large continuous memory blocks.

Insertions and Deletions: Inserting or deleting elements in an array can be inefficient, especially if we want to do so in the middle of the array. It often requires shifting all elements after the insertion or deletion point, which can be time-consuming for large arrays.

How Linked Lists overcome these disadvantages:

Linked lists are a dynamic data structure that can overcome the limitations of arrays in various ways:

Dynamic Size: Linked lists can grow or shrink dynamically as elements are added or removed. Each element in a linked list (called a node) contains a reference to the next node, allowing for flexibility in size.

Non-Contiguous Memory Allocation: Unlike arrays, linked lists do not require contiguous memory allocation. Each node can be located anywhere in memory, and they are connected through pointers or references. This makes better use of memory and reduces memory fragmentation.

Efficient Insertions and Deletions: Insertions and deletions in a linked list, especially at the beginning or middle, are more efficient compared to arrays. You can simply update the pointers or references to insert or delete elements without the need for shifting elements around.

Variable Element Sizes: Each node in a linked list can have a different size, allowing for more flexible data storage compared to arrays, where all elements must have the same size.

No Preallocation: Linked lists do not require preallocation of memory for a fixed number of elements, making them suitable for situations where the number of elements is unknown or can change over time.

(c) What is circular queue? Explain how insertion and deletion is done in circular queue with an example. (2+3=5)

Ans: A circular queue is a type of a queue in which the last element is followed by the first element. It is similar to the linear queue except that the last element of the queue is connected to the first element. In circular queue, the last element points to the first element making a circular link. As a result, a circle-like structure is formed.

A circular queue is the extended version of a regular (simple) queue where the last element is connected to the first element. Circular Queue is also known as Ring Buffer.

A circular queue can do what a linear queue can’t. The drawback that occurs in a linear queue is overcome by using the circular queue. If the empty space is available in a circular queue, the new element can be added in an empty space by simply incrementing the value of rear.

The main advantage of a circular queue over a simple queue is better memory utilization. If the last position is full and the first position is empty, we can insert an element in the first position. This is not possible in a linear queue.

(d) Show how the polynomial P(x)=7x²+15x³-2x²+9 can be represented using a linked list. (2)

Ans: To represent the polynomial P(x) = 7x^2 + 15x^3 – 2x^2 + 9 using a linked list, we can create a linked list where each node represents a term in the polynomial. Each node should contain two pieces of information: the coefficient and the exponent. Here’s how we can represent this polynomial as a linked list:

7x^2 + 15x^3 – 2x^2 + 9

Linked List Representation:

Node 1: Coefficient = 7, Exponent = 2

Node 2: Coefficient = 15, Exponent = 3

Node 3: Coefficient = -2, Exponent = 2

Node 4: Coefficient = 9, Exponent = 0 (assuming all other terms are included, including x^0)

In this representation, each node corresponds to a term in the polynomial:

Node 1 represents the term 7x^2.
Node 2 represents the term 15x^3.
Node 3 represents the term -2x^2.
Node 4 represents the constant term 9.

We can link these nodes together to create a linked list that represents the entire polynomial. Each node stores the coefficient and the exponent of its corresponding term, allowing you to work with and manipulate the polynomial using the linked list data structure.

3. (a) Consider the following binary search tree T (8)

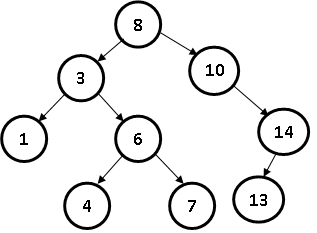
Draw the resulting binary search tree if the following operation is performed to the tree T

Insert element 19 in T
Insert element 15 in T
Insert element 2 in T
Delete element 14 from T
Delete element 3 from T

Ans:

(i) Insert 19

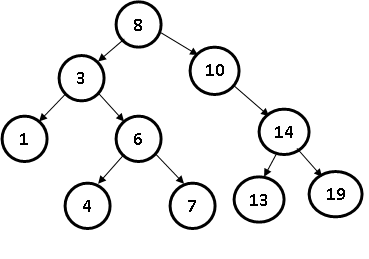
(ii) Insert 15

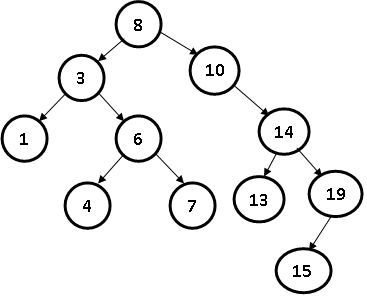
(iii) Insert 2

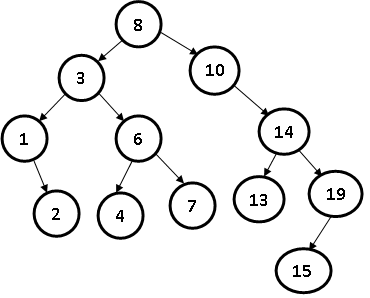
(b) Explain row and column major representation of a two dimensional array. (7)

Ans: In computer memory, a two-dimensional array can be stored in either a row-major or column-major representation. These representations determine the order in which elements of the array are stored in memory.

Row Major Representation:

In a row-major representation, also known as row-major order, the elements of a two-dimensional array are stored row by row. This means that all the elements of the first row are stored first, followed by the second row, and so on. In memory, it results in a contiguous block of elements belonging to the same row.

For example, consider a 2×3 array:

1 2 3

4 5 6

In a row-major representation, the elements would be stored in memory as follows:

1 2 3 4 5 6

Row-major representation is common in many programming languages like C, C++, and most low-level memory systems. It is well-suited for row-wise traversal of the array, making it efficient for operations that involve accessing or modifying entire rows.

Column Major Representation:

In a column-major representation, also known as column-major order, the elements of a two-dimensional array are stored column by column. This means that all the elements of the first column are stored first, followed by the second column, and so on. In memory, it results in a contiguous block of elements belonging to the same column.

Using the same 2×3 array:

1 2 3

4 5 6

In a column-major representation, the elements would be stored in memory as follows:

1 4 2 5 3 6

Column-major representation is less common than row-major representation but can be found in certain programming languages or environments. It is well-suited for column-wise traversal of the array and can be advantageous for operations that involve accessing or modifying entire columns.

4. (a) What is a binary tree? Mention some of the application of binary tree. (5)

Ans: A binary tree is a hierarchal data structure in which each node has at most two children. The Binary tree means that the node can have maximum two children. Here, binary name itself suggests that ‘two’; therefore, each node can have 0, 1 or 2 children.

A tree is called a binary tree if it has a finite set of nodes that is either empty or consists of a root and two disjoint subsets, each of which itself is a binary tree. The two subsets are called the left subtree and the right subtree of the original tree.

Binary trees are different from general trees. A binary tree has left and right subtrees, whereas, in general trees there is no left or right subtree.

Application of Binary Tree:

Binary trees have various applications in computer science and can be found in a wide range of algorithms and data structures.

Here are some common applications of binary trees:

Expression Evaluation: Binary trees can be used to represent and evaluate arithmetic expressions, such as mathematical formulas. This application is crucial in compilers and calculators.

Binary Tree Traversal: Binary trees are used for various traversal algorithms, such as inorder, preorder, and postorder traversals. These are fundamental in processing and searching binary tree data.

Balanced Binary Trees: Balanced binary trees, like AVL trees and Red-Black trees, ensure that the tree remains balanced, leading to efficient searching and insertion operations. They are commonly used in databases and file systems.

File Systems: Hierarchical file systems can be represented using binary trees. Directory structures, such as the File Allocation Table (FAT), can be organized as binary trees.

Game Trees: In games like chess or tic-tac-toe, binary trees can represent possible moves and game states. Game-playing algorithms like Minimax and Alpha-Beta Pruning use these trees to make decisions.

Binary Search: Binary trees can be employed in binary search algorithms to locate a specific item in a sorted list efficiently.

Optimal Binary Search Trees: In database indexing and information retrieval, optimal binary search trees are used to minimize the average search time for frequently accessed data.

Syntax Trees (Parse Trees): In compilers and natural language processing, binary trees are used to represent the syntax of a program or sentence for parsing and analysis.

Cryptography: Binary trees can be utilized in cryptographic algorithms, such as Merkle trees, for verifying data integrity and secure communication.

(b) The in order and post order traversal of a binary tree are as follows: (5)

In order: 4, 7, 2, 8, 5, 1, 6, 9, 3

Pre order: 1, 2, 4, 7, 5, 8, 3, 6, 9

Construct the binary tree

(c) Prove that for any non empty binary tree T if n₀ is the number of leaf node and n₂ is the number of internal node then n₀=n₂+1 (5)

5. (a) Consider the following sequence of operations on an empty stack. (5)

push(54); push(52); pop(); push(55); push(62); s=pop(), where push means insertion and pop means deletion

Also consider the following sequence of operations on an empty queue

enqueue(21); enqueue(24); dequeue(); enqueue(28); enqueue(32);

q=dequeue(); where enqueue means insertion and dequeue means deletion. Find the value of s+q.

(b) Mention some of the application of stack and queue. (5)

(c) Evaluate the following post fix expression using stack (5)

7 5 2 + * 4 1 5 – / –

6. (a) What is a graph? Explain how graph is represented in memory. (2+3=5)

Ans: A Graph is a non-linear data structure. It is a set of vertices connected by edges. A graph 𝐺 is defined as an ordered set (𝑉, 𝐸), where (𝐺) represents the set of vertices and (𝐺) represents the edges.

V(G) = set of vertices = {v1, v2, v3, …… vn }

E(G) = set of edges = {e1, e2, e3, ……en}

A Graph with 5 vertices v1, v2, v3, v4, v5 and 4 edges e1, e2, e3, e4 is shown in the following figure.

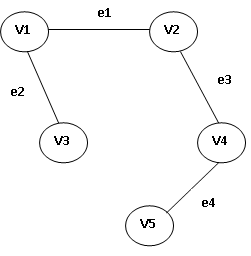
Graph Representation in Memory:

In data structure, a graph representation is a technique to store graph into the memory of computer. To represent a graph, we just need the set of vertices and for each vertex the neighbors of the vertex (vertices which is directly connected to it by an edge). If it is a weighted graph then that weight will be associated with each edge.

There are three standard ways to represent a graph in memory of a computer:

Adjacency Matrix
Adjacency List
Adjacency Multi List

Adjacency Matrix:

As the name suggests, the adjacency matrix is a matrix representation of a graph. An Adjacency Matrix is the simplest way to represent a graph.

An adjacency matrix is a two dimensional array of size V x V where V is the number of vertices in a graph. There are two possible values in each cell of the matrix: 0 and 1. 0 depicts that there is no path while 1 represents that there is a path.

The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph i.e. is there any edge connecting a pair of nodes in the graph.

Adjacency List Representation:

The adjacency list is another common representation of a graph. An adjacency list is a simple way to represent a graph as a list of vertices, where each vertex has a list of its adjacent vertices. In the adjacency list, we store a graph as a linked list structure. This representation is based on Linked Lists. In this approach, each Node is holding a list of Nodes, which are directly connected with that vertices. At the end of list, each node is connected with the null values to indicate that it is the end node of that list.

Adjacency Multi List:

An adjacency multi-list is a modified version of adjacency lists.Adjacency Multi-list is an edge-based rather than a vertex-based representation of graphs.

In multi-list representation of graphs, there are two parts, a directory of node information and a set of linked list of edge information.For each node of the graph, there is one entry in the node directory. The directory entry for node i point to a linked adjacency list for node i, each record of the linked list area appears on two adjacency lists: one for the node at each end of the represented edge.

In Adjacency Multi-list representation, following structure is used –

Link for Vi

Link for Vj

(b) What are graph traversal methods? Explain how depth first search works? (2+5=7)

Ans: Graph traversal is the process of visiting or updating each node (vertex) in a graph. Graph traversal methods are techniques used to visit and explore all the vertices and edges of a graph systematically. They are fundamental for solving various graph-related problems, such as finding paths, detecting cycles, and searching for specific elements within a graph.

There are two primary graph traversal methods:

(i) Breadth-First Search (BFS)

(ii) Depth First Search (DFS)

Depth First Search (DFS)

DFS is a graph traversal algorithm that explores as far as possible along a branch before backtracking. DFS traverses the graph vertically. It follows a path from starting node to an ending node then another path from start to end and so on until all the nodes are visited. DFS traverses a graph in depth ward motion and uses stack data structure.

(c) What is spanning tree? Mention some of the application of spanning tree. (1+2=3)

Ans: A spanning tree is a fundamental concept in graph theory and network design. It is a subgraph of a connected, undirected graph that includes all the vertices of the original graph while minimizing the number of edges. In other words, a spanning tree of a graph is a tree that spans all the vertices in the graph, connecting them in a way that there are no cycles.

Applications:

Network Design: Spanning trees are used in designing efficient network topologies, such as in computer networks and communication systems, to ensure connectivity while minimizing the number of links.

Algorithm Design: Spanning trees are used as a key component in various algorithms, including minimum spanning tree algorithms like Kruskal’s and Prim’s algorithms, which help find the minimum-cost subgraph that spans all vertices in weighted graphs.

Graph Visualization: Spanning trees are often used to visualize comcplex graphs more clearly by simplifying the structure while preservng connectivity.

There can be multiple spanning trees for a given graph, depending on which edges are included or excluded. However, all spanning trees for the same graph will have the same number of vertices and will maintain connectivity while being acyclic.

Spanning trees are a fundamental concept in graph theory, and they play a crucial role in various real-world applications where network design, connectivity, and optimization are important considerations.

7. (a) Using Prim’s algorithm construct a minimum spanning tree of the following graph starting with node A. (8)

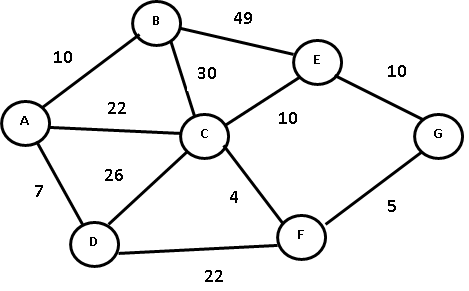
Ans:

(b) What is internal sort algorithm? Explain how bubble sort algorithm works with an example? (2+5=7)

Ans: An internal sort algorithm, also known as an “in-memory sort algorithm,” is a type of sorting algorithm that operates entirely within the computer’s main memory (RAM). These algorithms are designed to efficiently rearrange the elements of an array or a data structure, such as a list or an array, without relying on external storage or additional memory.

Internal sorting is typically used for relatively small datasets that can be loaded entirely into RAM. It is contrasted with external sorting, which is used for larger datasets that cannot fit entirely in memory and require the use of external storage devices, such as hard drives, to perform the sorting operation.

Bubble Sort is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements until they are not in the intended order. The algorithm traverses a list and compares adjacent values, swapping them if they are not in the correct order.

The algorithm continues this process until no more swap is needed, indicating that the list is sorted. It’s called “bubble sort” because the smaller elements “bubble” to the top of the list as the algorithm progresses.

Here’s how the bubble sort algorithm works with an example:

Suppose we have an unsorted list of integers:

5, 2, 9, 3, 6

First Pass:

Compare the first two elements (5 and 2). Since 5 is greater than 2, swap them.

2, 5, 9, 3, 6

Compare the next two elements (5 and 9). They are in the correct order, so no swap is needed.

2, 5, 9, 3, 6

Continue this process until we reach the end of the list. After the first pass, the largest element (9) has “bubbled” to the end of the list.

Second Pass:

Repeat the same process, but this time, ignore the last element (9) because it is already in its correct position.

Compare the first two elements (2 and 5). They are already in the correct order.

Compare the next two elements (5 and 3). Swap them since 5 is greater than 3.

2, 3, 5, 9, 6

Continue until you reach the second-to-last element. After the second pass, the second-largest element (5) has “bubbled” to its correct position.

Third Pass:

Repeat the process again, but ignore the last two elements (9 and 6) since they are already in their correct positions.
Compare the first two elements (2 and 3). They are already in the correct order.
No more swaps are needed.

Fourth Pass:

Continue with the same process, but ignore the last three elements (9, 6, and 5).
Compare the first two elements (2 and 3). They are already in the correct order.
No more swaps are needed.

Fifth Pass:

Continue with the same process, but ignore all elements except the first one.
No swaps are needed.

Since no swaps are needed in the fifth pass, the algorithm terminates. The list is now sorted:

2, 3, 5, 6, 9

Bubble sort is straightforward to understand and implement but is not very efficient for large lists. Its average and worst-case time complexity is O(n^2), where n is the number of elements in the list. There are more efficient sorting algorithms available for larger datasets, such as quicksort or merge sort.

Total Views: 229