Distributed Mutual Exclusion |Mutual Exclusion in Distributed System

Introduction:

Distributed Mutual Exclusion (DME) is a critical problem in distributed systems where multiple processes or nodes compete for access to shared resources. Distributed processes often need to coordinate their activities. If a collection of processes share a resource or collection of resources, then often mutual exclusion is required to prevent interference and ensure consistency when accessing the resources. Mutual exclusion ensures that at a time only one of the concurrent processes are allowed to access the common or shared resources. In case of distributed systems, where multiple sites are considered it is named as distributed mutual exclusion (DME).

Mutual exclusion is a fundamental problem in distributed computing systems. Mutual exclusion ensures that concurrent access of processes to a shared resource or data is serialized, that is, executed in a mutually exclusive manner. Mutual exclusion in a distributed system states that only one process is allowed to execute the critical section (CS) at any given time. In a distributed system, shared variables (semaphores) or a local kernel cannot be used to implement mutual exclusion. Distributed mutual exclusion is based on message passing.

Requirements of Mutual Exclusion:

In a distributed system, mutual exclusion refers to the property that ensures only one process at a time can access a critical section, thereby preventing concurrent access that could lead to data corruption or inconsistency. Achieving mutual exclusion in a distributed environment poses several requirements to ensure the correctness and efficiency of the system:

Safety: The foremost requirement of mutual exclusion is safety, meaning that only one process is allowed to execute within the critical section at any given time. This ensures that conflicting operations do not occur simultaneously, preventing data corruption or integrity issues.

Liveness: While ensuring safety, mutual exclusion algorithms should also guarantee liveness, meaning that processes are eventually allowed to enter the critical section if they request access. This ensures progress in the system and prevents deadlock scenarios where processes are indefinitely blocked from entering the critical section.

Fairness: Mutual exclusion algorithms should aim to provide fairness among processes, ensuring that every process eventually gets a chance to access the critical section. Unfairness can lead to starvation, where some processes are continually denied access, resulting in a degradation of system performance.

Decentralization: In distributed systems, mutual exclusion algorithms should be decentralized to reduce dependencies on central authorities or single points of failure. Decentralization promotes scalability, fault tolerance, and resilience in the face of failures or network partitions.

Efficiency: Mutual exclusion algorithms should be efficient in terms of message complexity, computation overhead, and resource utilization. They should minimize contention and avoid unnecessary delays or bottlenecks that could degrade system performance.

Fault Tolerance: Distributed systems are prone to failures, such as process crashes, message losses, or network partitions. Mutual exclusion algorithms should be resilient to such failures, ensuring that the system remains operational and consistent even in the presence of faults.

Synchronization: Mutual exclusion algorithms often rely on synchronization mechanisms to coordinate access to the critical section among processes. These mechanisms should be robust and efficient, ensuring that processes coordinate effectively without introducing unnecessary overhead or complexity.

Algorithms for Mutual Exclusion:

There are several algorithms for achieving distributed mutual exclusion, each with its own approach and characteristics. Here are some common approaches:

Token-Based Algorithms: In token-based algorithms, a special token is passed among processes to grant permission for accessing the critical section. Only the process holding the token can enter the critical section. Examples of token-based algorithms include the Suzuki-Kasami algorithm, Raymond’s Algorithm.

Timestamp-Based Algorithms: Timestamp-based algorithms assign a unique timestamp to each process. Processes request access to the critical section based on their timestamps, with the lowest timestamp being given priority. Timestamps are updated dynamically to ensure fairness and prevent starvation. Examples of timestamp-based algorithms include the Ricart-Agrawala Algorithm, Lamport’s algorithm.

Quorum-Based Algorithms: Quorum-based algorithms divide processes into groups or quorums, where each quorum has the authority to grant access to the critical section. A process must obtain permission from a quorum before entering the critical section. Examples of quorum-based algorithms include the Chandy-Lamport algorithm and the Bully algorithm.

Voting-Based Algorithms: Voting-based algorithms use voting or agreement mechanisms among processes to determine which process can enter the critical section. Processes cast votes or participate in rounds of voting until a consensus is reached on granting access to the critical section. Examples of voting-based algorithms include the Maekawa’s Algorithm , Chang-Roberts algorithm and the LeLann-Gallager algorithm.

Centralized Coordinator: In this approach, a centralized coordinator process is responsible for managing access to the critical section. Processes send requests to the coordinator, which grants access based on a predefined policy. While simple to implement, this approach can introduce a single point of failure and scalability issues.

The Central Server Algorithm:

The central server algorithm can be seen as a token based algorithm. The system maintains one token and make sure that only one process at a time gets that token. A process has not enter the critical section if it doesn’t have a token. The “token” in this case is effectively the permission or authorization granted by the central server to access the critical section.

The simplest way to achieve mutual exclusion is to employ a server that grants permission to enter the critical section. To enter a critical section, a process sends a request message to the server and awaits a reply from it. Conceptually, the reply constitutes a token signifying permission to enter the critical section. If no other process has the token at the time of the request, then the server replies immediately, granting the token. If the token is currently held by another process, then the server does not reply, but queues the request.

When a process exits the critical section, it sends a message to the server, giving it back the token. If the queue of waiting processes is not empty, then the server chooses the oldest entry in the queue, removes it and replies to the corresponding process. The chosen process then holds the token.

In short, the Central Server Algorithm works as follows:

· A server serves as the coordinator for the CS

· Any process that needs to access the CS sends a request to the coordinator

· The coordinator puts requests in a queue in the order it receives them and grants permission to the process that is at the head of the queue

· When a process exits the CS, it sends a release message to the coordinator

In the above figure, we show a situation in which p₂ ’s request has been appended to the queue, which already contained p₄’s request. p₃ exits the critical section, and the server removes p₄ ’s entry and grants permission to enter to p₄ by replying to it. Process p₁ does not currently require entry to the critical section.

A Ring-Based Algorithm:

A ring-based algorithm for distributed mutual exclusion (DME) is a type of algorithm where processes in a distributed system are organized in a logical ring , and access to a critical section is controlled by passing a token around the ring. Each process holds a token, and only the process possessing the token is allowed to enter the critical section. When a process is done with the critical section, it passes the token to its successor in the ring.

If a process receives the token and does not need to access the CS, it immediately forwards the token to its neighbour. A process that requires the token waits until it receives it. To exit the critical section, the process sends the token to its neighbour. This algorithm continuously consumes network bandwidth (except when a process is inside the critical section), the processes send messages around the ring even when no process requires entry to the critical section.

Here’s a basic outline of how a ring-based DME algorithm could work:

1. Initialization: Processes in the distributed system are organized in a logical ring topology. Each process has a unique identifier and knows its successor in the ring.
2. Token Management: Initially, a token is arbitrarily assigned to one of the processes in the ring. This process is typically designated as the initial token holder.
3. Requesting Access: When a process wants to enter the critical section, it must possess the token. If the process does not have the token, it sends a request message to its successor in the ring, asking for the token.
4. Token Passing: Upon receiving a request message, a process checks whether it currently holds the token. If it does, it grants the token to the requesting process. If not, it forwards the request message to its own successor in the ring.
5. Entering Critical Section: Once a process receives the token, it enters the critical section and performs its required operations. It then releases the token by passing it to its successor in the ring.
6. Exiting Critical Section: After completing the critical section, the process releases the token and resumes normal operation.
7. Token Circulation: The token continues to circulate around the ring, allowing processes to take turns entering the critical section in a fair and orderly manner.

Ricart Agrawala Algorithm:

The Ricart-Agrawala algorithm is a distributed mutual exclusion algorithm that allows processes in a distributed system to gain exclusive access to a critical section. It was proposed by Glenn Ricart and Ashok Agrawala in 1981. The algorithm is based on message passing and uses a request-grant mechanism to ensure mutual exclusion.

In the Ricart-Agrawala Algorithm, processes request access to a critical section by sending messages to each other. The algorithm relies on timestamps to establish a partial ordering of requests, ensuring fairness and preventing deadlock. Each process maintains a queue of pending requests and grants access based on the timestamp of the requests.

The basic idea is that processes that require entry to a critical section multicast a request message, and can enter it only when all the other processes have replied to this message. The Ricart-Agrawala algorithm ensures that processes enter the critical section in timestamp order, thereby achieving mutual exclusion. It also guarantees safety, meaning that no two processes will simultaneously execute their critical sections.

Here’s a brief overview of how the Ricart-Agrawala algorithm works:

1. Initialization: Each process in the distributed system maintains a queue to hold incoming requests for accessing the critical section. Each process also maintains a local clock or timestamp.
2. Requesting Access: When a process wants to enter the critical section, it sends a request message to all other processes in the system. The request message includes the process’s timestamp, indicating its priority.
3. Receiving Requests: Upon receiving a request message from another process, a process compares the timestamp of the request message with its own timestamp. If the received request has a lower timestamp (indicating higher priority), the process can grant immediate access to its critical section. If the request has a higher timestamp, the process adds the request to its queue and sends a reply to the requesting process.
4. Granting Access: If a process receives replies from all other processes in the system and it has the highest priority (i.e., the lowest timestamp) among all pending requests, it can enter the critical section.
5. Exiting the Critical Section: After completing its work in the critical section, the process sends release messages to all other processes, indicating that it has exited the critical section.
6. Handling Requests and Replies: Upon receiving a release message, a process removes the corresponding request from its queue. When a process receives a reply message, it updates its set of outstanding replies.

The algorithm is given below:

On initialization

state := RELEASED;

To enter the critical section

state := WANTED;

Multicast request to all processes;

 T := request’s timestamp;

Wait until (number of replies received = (N – 1));

state := HELD;

On receipt of a request <T_i, pi> at pj (I = j) if (state = HELD or (state = WANTED and (T, pj) < (Ti, pi)))

then

queue request from pi without replying;

else

reply immediately to pi;

end if

To exit the critical section

state := RELEASED;

reply to any queued requests;

Each process records its state of being outside the critical section (RELEASED), wanting entry (WANTED) or being in the critical section (HELD) in a variable state. 

If a process requests entry and the state of all other processes is RELEASED, then all processes will reply immediately to the request and the requester will obtain entry. If some process is in the state HELD, then that process will not reply to requests until it has finished with the critical section, and so the requester cannot gain entry in the meantime. If two or more processes request entry at the same time, then whichever process’s request bears the lowest timestamp will be the first to collect N – replies, 1 granting it entry next.

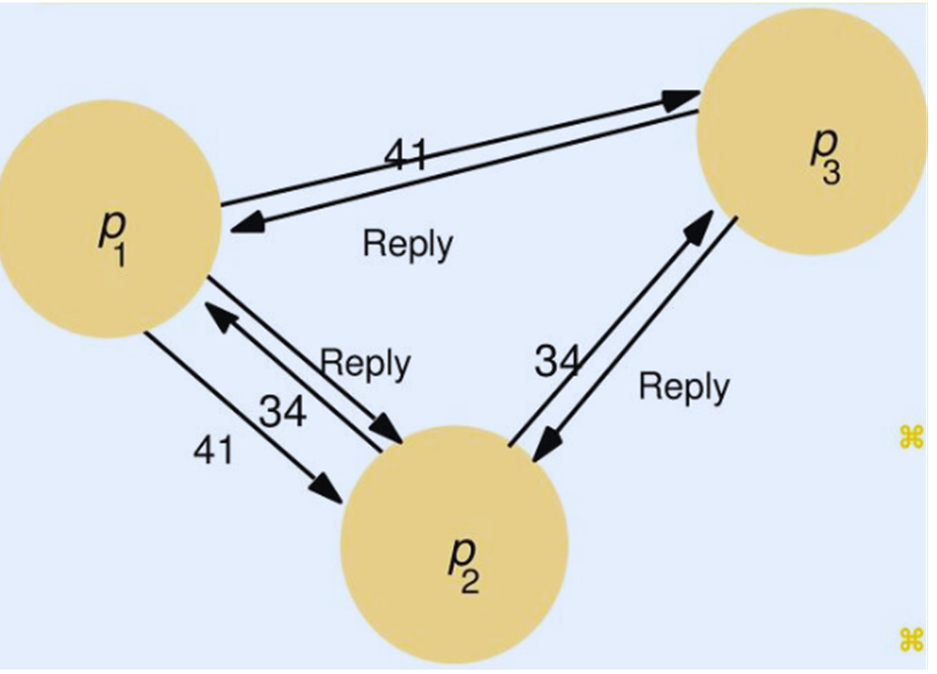
To illustrate the algorithm, consider a situation involving three processes, p₁ , p₂ and p₃ , shown in Figure above. Let us assume that p₃ is not interested in entering the critical section, and that p₁ and p₂ request entry concurrently. The timestamp of p₁’s request is 41, and that of p₂ is 34. When p₃ receives their requests, it replies immediately. When p₂ receives p₁’s request, it finds that its own request has the lower timestamp and so does not reply, holding p₁ off. However, p₁ finds that p₂’s request has a lower timestamp than that of its own request and so replies immediately. On receiving this second reply, p₂ can enter the critical section. When p₂ exits the critical section, it will reply to p₁’s request and so grant it entry.

To Enter Critical Section:

· When a process p_i wants to enter the critical section, it sends a time-stamped REQUEST message to all other process (Multicasting).

· When a process p_j receives a REQUEST message from process p_i, it sends a REPLY message to process p_i if and only if:

o  Process p_j neither requesting nor currently executing the critical section.

o  In case process p_j requesting, the timestamp of process p_i’s request is smaller than its own request. Otherwise the request is deferred by process p_j.

To Execute Critical Section:

 · Process p_i enters the critical section if it has received the REPLY message from all process.

To Release the Critical Section:

·  Upon exiting process p_i sends REPLY message to all deferred requests.

Maekow’s Voting Algorithm:

Maekawa’s Algorithm is an algorithm for achieving mutual exclusion in a distributed system. It is a deadlock free algorithm that ensures that only one process can enter the critical section at any given time. The algorithm allows multiple processes to access a shared resource without interfering with each other. It is based on the concept of quorum. Maekawa’s Algorithm is actually considered a quorum-based algorithm, rather than a pure voting-based algorithm. It utilizes a voting mechanism within each quorum to determine access to the critical section.

In Maekawa’s Algorithm, processes are organized into a set of disjoint quorums. Each process can grant permission to enter the critical section to other processes within its quorum. A process can enter the critical section only when it has received permission from all processes in its quorum. This algorithm utilizes a voting mechanism within the quorums to determine access to the critical section.

Maekawa’s Algorithm ensures mutual exclusion by guaranteeing that only one process from each quorum can access the critical section simultaneously. This allows for efficient utilization of resources while preventing race conditions and conflicts.

A quorum is defined as a set of processes that satisfies two conditions:

· Any two quorums have at least one process in common.

· The intersection of all quorums is non-empty.

Here’s a brief overview of Maekawa’s Algorithm:

1. Partitioning into Quorums: The system’s processes are divided into several disjoint subsets or quorums. Each quorum consists of a subset of processes.
2. Voting within Quorums: When a process wants to enter the critical section, it sends a request to all processes within its quorum.
3. Quorum Voting: Each process in the quorum votes on whether the requesting process can enter the critical section based on certain criteria. Typically, the criteria involve ensuring that only one process at a time from each quorum enters the critical section.
4. Granting Access: If the requesting process receives enough affirmative votes from its quorum, it can enter the critical section.
5. Releasing Access: Once a process completes its critical section execution, it releases access, allowing another process to enter.